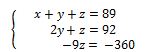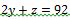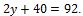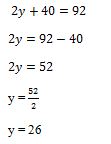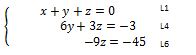Leçon, Résoudre un système d'équations à 3 inconnus avec la méthode du pivot

Blog Single

Exercice

Résoudre les systèmes d’équations suivants par la méthode du pivot.

 

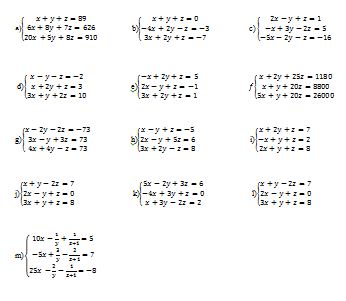
Correction de l’exercice

Résolution des exercices par la méthode du pivot


 
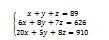
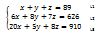
          Pour traiter un exercice comme celui-ci avec la méthode du Pivot, on commence par nommer les lignes. Certains utiliseront E1, E2 et E3 pour dire équation 1, équation 2 et équation 3. D’autres vont utiliser L1, L2 et L3 pour signifier : ligne 1, ligne 2 et ligne 3. Voici comment sera notre système quand le nomme.


         Une fois qu’on a nommé les lignes, on choisit un pivot parmi ces lignes. Les élèves préfèrent souvent choisir la ligne 1. Cette ligne est appelée pivot parce qu’on l’utilise pour annuler les inconnues dans les autres lignes. Il y a trois inconnues dans notre système, ce qui nous complique la tâche. On ne peut pas trouver les trois inconnus une fois. Il faut donc supprimer certains inconnus sur les équations pour nous concentrer sur un ou deux inconnus. Le pivot nous permet justement de supprimer un inconnu dans les lignes suivantes. On peut choisir de supprimer les x, les y ou les z. Pour que cela ne nous embrouille pas, commençons par supprimer les x.

         Que constatons-nous ? Il y a 1 seul x à la ligne pivot ( . Sur la ligne 2, nous avons 6 x. Que faire pour annuler les x sur les deux lignes ? Généralement, on permute les nombres qui sont devant x sur les deux lignes, les x s’annulent. Si nous ajoutons le nombre 6 (qui est devant x de la ligne 2) à la ligne 1 (L1) qui est la ligne pivot, nous aurons aussi 6 x à la ligne pivot, et si nous multiplions la ligne 2 par le 1 qui est devant x de la ligne 1, nous aurons aussi 6 x à la ligne 2 (L2). En les additionnant on aura 12 x. Les x ne vont pas toujours s’annuler.

Que faire ? Il faut jouer avec les signes. Si le pivot et la ligne où on doit supprimer l’inconnu sont de signes opposés, on se contente juste de permuter les nombres devant x de la ligne 1 et de la ligne 2. Si, comme c’est le cas ici, la ligne pivot et la ligne où on doit supprimer notre inconnu sont de mêmes signes, alors on ajoute un signe négatif sur l’une des deux lignes pour faciliter l’annulation. On préfère ajouter le signe (-) à la ligne pivot.

On va donc poser cette équation : -6 L1 + 1 L2



Cela veut tout simplement dire qu’on multiplie la ligne 1 par -6 et la ligne 2 par 1.

On aura donc ceci :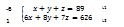               

Faisons la multiplication. Celui qui est dehors (hors des accolades) multiplie tous ceux qui sont à l’intérieur. -6 va donc multiplier toute la ligne 1, et 1 va aussi multiplier toute la ligne 2. A la ligne 1,     -6 va donc multiplier x, y, z et 89. A la ligne 2, 1 va multiplier 6x, 8y, 7z et 626.

On aura donc cette équation :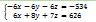  

Vous vous êtes rendu compte que les signes se sont multipliés aussi.                

Bref rappel : -x+=- (-multiplié par + est égale à -). -x- = + (- multiplié par - donne +). +x+ = +      (+ multiplié par + est égale à plus). Vous devez savoir ces bases de la mathématique.

Une fois qu’on a fait ces multiplications, on fait donc l’addition des deux lignes pour trouver une autre ligne sans x, que nous allons appeler la ligne 4 (L4).

Voici cette addition :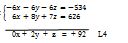  

Que s’est-il passé ? Nous avons juste additionné les x, les y, les z et les nombres qui n’ont pas d’inconnus entre eux.

Faisons encore un rappel dans l’addition. Pour additionner deux nombres, on met d’abord le signe du plus grand. Si les nombres sont de mêmes signes, on fait l’addition. S’ils sont de signes opposés, on fait la soustraction. Prenons l’exemple des y dans notre équation. Pour calculer les y, on avait -6y et 8y. Entre les deux, 8 est plus grand, et son signe est +. On maintient donc le signe + pour la solution. Puisque -6 et 8 sont de signes opposés (- et +), on a fait la soustraction (8-6), qui nous a donné 2y de la solution. C’est pourquoi sur la colonne des y on a eu + 2y.


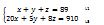
Une fois que nous avons la ligne 4, nous utilisons encore notre pivot (attention ! On ne change pas de ligne pivot). Puisque nous avons choisi la ligne 1 comme pivot, on va utiliser la même ligne pour supprimer x sur la troisième ligne.

 

En ajoutant -20 à la première ligne et 1 à la troisième ligne, on annule les x dans la ligne 1 et la ligne 3. On aura donc ceci : -20 L1 + 1 L3

      

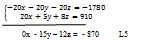
Nous avons donc deux lignes de plus sans x, seulement avec les y et z. En effet, les lignes 4 (L4) et les lignes 5 (L5) ne possèdent pas de x, mais seulement de y et de z. Le pivot nous a donc permis d’annuler un inconnu. On a donc les nouvelles équations cette fois avec deux inconnus au lieu de trois. On va donc réunir ces deux équations pour annuler encore un inconnu (entre y et z). On va chercher à annuler les y.
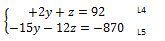
  On aura donc ce nouveau système d’équations :

On va chercher à annuler soit les y, soit les z dans ce nouveau sytème. Annulons les y. La méthode est la même. Puisqu’ils sont de signes opposés, on permute juste leurs nombres. On envoie 15 pour multiplier la ligne 4 et 2 pour multiplier la ligne 5. Cela donne ceci :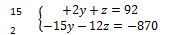

Ce qui donne ceci: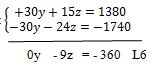

A ce niveau on fait la triangulation. On maintient notre pivot, on choisit la ligne 4 ou la ligne 5, et on y ajoute la ligne 6. Prenons la ligne 4. On a ceci :


On parle de triangulation parce qu’à ce niveau, notre système ressemble à un triangle. A la ligne 6 on a désormais un seul inconnu qui est z. On peut donc très facilement tirer sa valeur.

-9z = -360   L6

z=
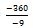
   z = 40.

Comme vous avez le signe négatif au numérateur et au dénominateur d’une fraction, les deux s’annulent.

Nous avons donc notre inconnu z qui est 40.

On revient à notre équation triangulée, on prend la ligne 4 et on y remplace z par sa valeur pour trouver y. On a donc :  En remplaçant z par sa valeur, nous aurons :      Nous rassemblons ceux qui se ressemblent. Quand 40 va traverser l’égalité, il change de signe (Tout nombre qui traverse l’égalité ou l’inégalité pour aller de l’autre coté change de signe). Nous aurons donc :

 

Nous avons déjà y et z. Nous allons sur la ligne 1 de notre système d’équations triangulé pour remplacer y et z par leurs valeurs respectives afin de trouver x.

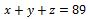Remplaçons y et z par leurs valeurs.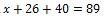


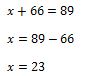
Nous avons déjà les trois inconnus. Nous allons donc présenter l’ensemble solution. Il se présente comme ceci :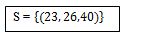 

Il est mieux d’encadrer votre ensemble solution. Pour écrire la solution, on commence par écrire x, puis y et on finit par z.

On va traiter les autres exercices sans plus entrer en détail, puisque vous savez déjà comment on traite. Il est préférable de traiter les autres au brouillon et revenir vérifier la correction et voir si vous avez bien compris. Rappelons que cet exercice est corrigé gratuitement pour vous par le parti politique camerounais la LIMARA (Ligue des Masses pour la Renaissance Africaine) et son organisation soeure la Ligue Associative Africaine. Allez et exercez-vous dans d’autres matières à notre site web www.ligueaa.org ou à notre chaine youtube : Ligue Associative Africaine.




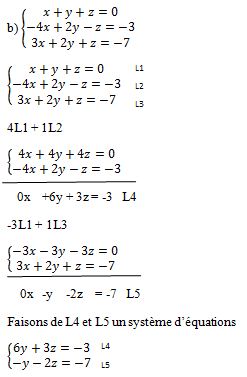
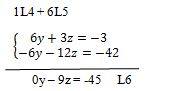
Triangulons notre système


Tirons la valeur de z dans L6

-9z=-45

  z= 5

z dans L4 pour tirer la valeur de x

6y + 3z = -3

6y + 3 (5) = -3

6y + 15 = -3

6y=-3-15

6y=-18

y=     y=-3

y et z dans L1 pour tirer la valeur de x

x+y+z=0

x+(-3)+5=0

x-3+5=0

x+2=0
x=-2

 

 
Méthode de vérification. Si vous voulez savoir si vous avez trouvé, vérifiez les inconnus trouvés sur chaque ligne du système. Vos réponses doivent vérifier toutes les lignes du système. Faisons une vérification.


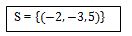
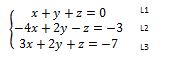
L1 : x+y+z=0       -2+(-3)+5=0         -2-3+5=0      -5+5=0        0=0   La ligne 1 vérifie

L2 : -4x+2y-z=-3    -4(-2)+2(-3)-5=-3     +8-6-5=-3    +8-11=-3    -3=-3    La ligne 2 vérifie

L3 : 3x+2y+z=-7    3(-2)+2(-3)+5=-7    -6-6+5=-7     -12+5=-7      -7=-7  La ligne 3 vérifie aussi.

Toutes les lignes vérifient nos réponses, donc nous avons trouvé. Attention ! Cette vérification n’entre pas sur votre feuille de composition. Elle n’est pas nécessaire. Vous l’utilisez si vous doutez de vos réponses.

La LIMARA, la Ligue Associative Africaine et moi, pour ne pas rendre ce travail trop long, allons juste vous donner les réponses des autres exercices. Vous savez déjà comment résoudre un système à trois inconnus en utilisant la méthode du pivot.

Voici les autres systèmes et leurs ensembles solution


 

Vous vous demandez sûrement comment on a traité le système d’équations m). Nous allons le traiter pour que vous compreniez. N’oubliez pas d’aller dans notre site web www.ligueaa.org pour avoir vos cours, les exercices et les fiches de travaux dirigés, ou bien de vous rendre dans notre chaine youtube appelée Ligue Associative Africaine. Revenons à notre système.




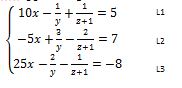
N’oubliez pas d’aller dans le site web www.ligueaa.org. Vous pouvez intégrer un des groupes de préparation aux examens officiels piloté par la LIMARA et la Ligue Associative Africaine ou bien vous inscrire aux formations diverses en envoyant votre numéro whatsapp au +237 674471831 ou au +237 696366502.

Pour ceux qui veulent fructifier leurs revenus, vous pouvez aussi investir dans nos sociétés en contactant les mêmes numéros. Bonne chance pour vos examens.